Ecuación de Regresión Logística en R: Entendiendo la Fórmula con Ejemplos

Name

Rajiv Chandra

Published on 20/4/2022

(opens in a new tab) (opens in a new tab) (opens in a new tab) (opens in a new tab) (opens in a new tab) (opens in a new tab)

La regresión logística es una de las técnicas estadísticas más populares utilizadas en el aprendizaje automático para problemas de clasificación binaria. Utiliza una función logística para modelar la relación entre una variable dependiente y una o más variables independientes. El objetivo de la regresión logística es encontrar la mejor relación entre las características de entrada y la variable de salida. En este artículo, discutiremos la ecuación de regresión logística con ejemplos en R.

¿Quieres crear rápidamente visualización de datos desde un marco de datos de Python Pandas sin código?

PyGWalker es una biblioteca de Python para el análisis exploratorio de datos con visualización. PyGWalker (opens in a new tab) puede simplificar tu flujo de trabajo de análisis de datos y visualización de datos en Jupyter Notebook, convirtiendo tu marco de datos de pandas (y marco de datos de polars) en una interfaz de usuario estilo Tableau para la exploración visual.

(opens in a new tab)

Ecuación de Regresión Logística

La ecuación de regresión logística se puede definir de la siguiente manera:

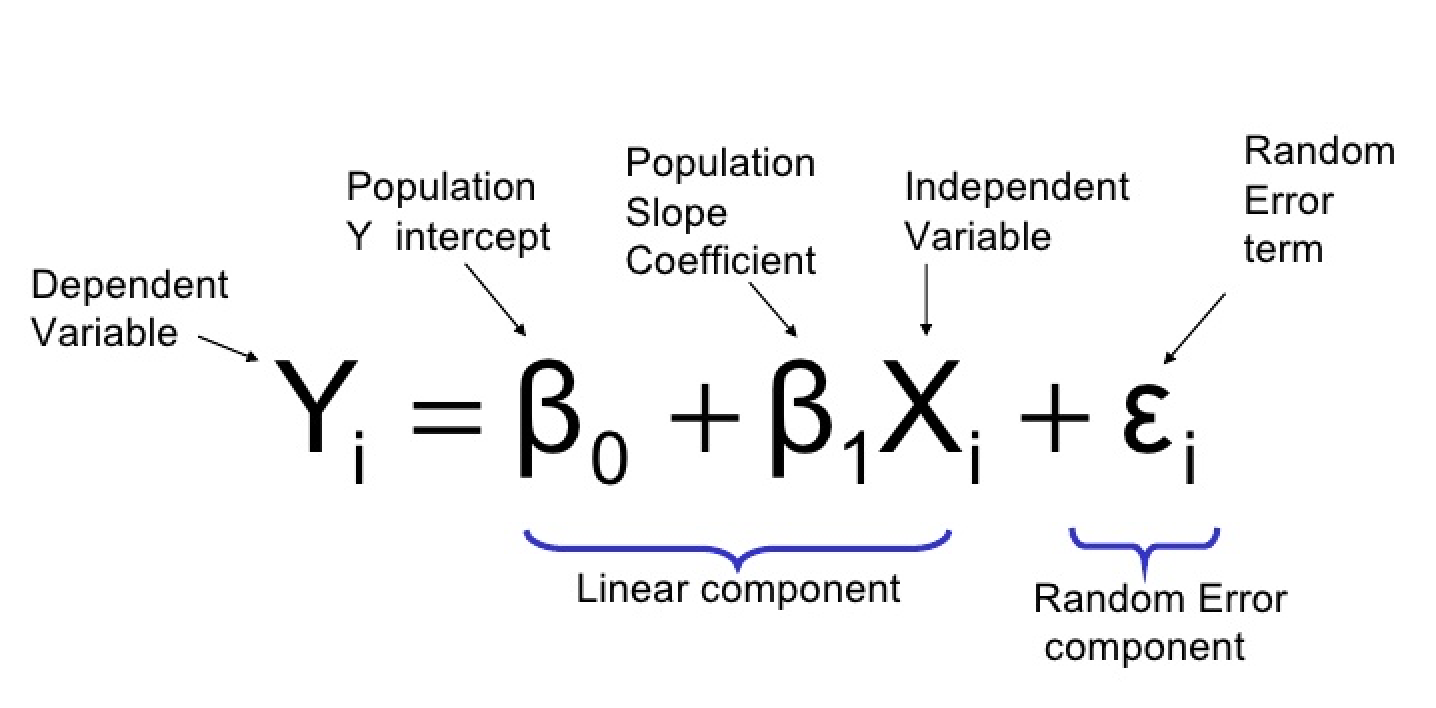
donde:

• Y: la variable dependiente o variable de respuesta (binaria)
• X1, X2, …, Xp: variables independientes o predictores
• β0, β1, β2, …, βp: coeficientes beta o parámetros del modelo

El modelo de regresión logística estima los valores de los coeficientes beta. Los coeficientes beta representan el cambio en el log-odds de la variable dependiente cuando la variable independiente correspondiente cambia en una unidad. La función logística (también llamada función sigmoide) transforma los log-odds en probabilidades entre 0 y 1.

Aplicando la Regresión Logística en R

En esta sección, utilizaremos la función glm() en R para construir y entrenar un modelo de regresión logística en un conjunto de datos de muestra. Utilizaremos el conjunto de datos hr_analytics del paquete RSample.

Cargando los Datos

Primero, cargamos el paquete y el conjunto de datos requeridos:

library(RSample)
data(hr_analytics)

El conjunto de datos hr_analytics contiene información sobre empleados de una empresa en particular, incluyendo su edad, género, nivel educativo, departamento y si dejaron la empresa o no.

Preparando los Datos

Convertimos la variable objetivo left_company en una variable binaria:

hr_analytics$left_company <- ifelse(hr_analytics$left_company == "Yes", 1, 0)

Luego, dividimos el conjunto de datos en conjuntos de entrenamiento y prueba:

set.seed(123)
split <- initial_split(hr_analytics, prop = 0.7)
train <- training(split)
test <- testing(split)

Construyendo el Modelo

Ajustamos un modelo de regresión logística utilizando la función glm():

logistic_model <- glm(left_company ~ ., data = train, family = "binomial")

En este ejemplo, utilizamos todas las variables independientes disponibles (edad, género, educación, departamento) para predecir la variable dependiente (left_company). El argumento family especifica el tipo de modelo que queremos ajustar. Dado que estamos tratando con un problema de clasificación binaria, especificamos "binomial" como la familia.

Evaluando el Modelo

Para evaluar el rendimiento del modelo, utilizamos la función summary():

summary(logistic_model)

Resultado:

Call: 
glm(formula = left_company ~ ., family = "binomial", data = train)

Deviance Residuals: 
   Min      1Q  Median      3Q     Max  
-2.389  -0.640  -0.378   0.665   2.866  

Coefficients:
                     Estimate Std. Error z value Pr(>|z|)    
(Intercept)         -0.721620   0.208390  -3.462 0.000534 ***
age                 -0.008328   0.004781  -1.742 0.081288 .  
genderMale           0.568869   0.086785   6.553 5.89e-11 ***
educationHigh School 0.603068   0.132046   4.567 4.99e-06 ***
educationMaster's   -0.175406   0.156069  -1.123 0.261918    
departmentHR         1.989789   0.171596  11.594  < 2e-16 ***
departmentIT         0.906366   0.141395   6.414 1.39e-10 ***
departmentSales      1.393794   0.177948   7.822 5.12e-15 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 6589.7  on 4799  degrees of freedom
Residual deviance: 5878.5  on 4792  degrees of freedom
AIC: 5894.5

Number of Fisher Scoring iterations: 5

El resultado muestra los coeficientes del modelo (coeficientes beta), sus errores estándar, valor z y valor p. Podemos interpretar los coeficientes de la siguiente manera:

• Los coeficientes con un valor p significativo (p < 0.05) son estadísticamente significativos y tienen un impacto significativo en el resultado. En este caso, la edad, el género, la educación y el departamento son predictores significativos de si un empleado deja la empresa o no.
• Los coeficientes con un valor p no significativo (p > 0.05) no son estadísticamente significativos y no tienen un impacto significativo en el resultado. En este caso, el nivel educativo (Master's) no es un predictor significativo.

Realizando Predicciones

Para hacer predicciones sobre nuevos datos, utilizamos la función predict():

predictions <- predict(logistic_model, newdata = test, type = "response")

El argumento newdata especifica los nuevos datos sobre los cuales queremos hacer predicciones. El argumento type especifica el tipo de salida que queremos. Dado que estamos tratando con una clasificación binaria, especificamos "response" como el tipo.

Evaluando las Predicciones

Finalmente, evaluamos las predicciones utilizando la matriz de confusión:

table(Predicted = ifelse(predictions > 0.5, 1, 0), Actual = test$left_company)

Resultado:

         Actual
Predicted    0    1
        0 1941  334
        1  206  419

La matriz de confusión muestra el número de verdaderos positivos, falsos positivos, verdaderos negativos y falsos negativos. Podemos utilizar estos valores para calcular métricas de rendimiento como precisión, exhaustividad y puntuación F1.

Conclusión

En este artículo, discutimos la ecuación de regresión logística y cómo se utiliza para modelar la relación entre variables independientes y una variable binaria dependiente. También demostramos cómo utilizar la función glm() en R para construir, entrenar y evaluar un modelo de regresión logística en un conjunto de datos de muestra. La regresión logística es una técnica poderosa para problemas de clasificación binaria y se utiliza ampliamente en el aprendizaje automático.