파이썬에서의 차원 축소: 알아야 할 상위 팁
- Name
- Oluwaseun Adeojo
Published on
파이썬에서의 차원 축소에 대한 포괄적인 가이드에 오신 것을 환영합니다. 데이터 중심의 시대에서는 고차원 데이터셋을 다루는 능력이 모든 데이터 과학자에게 필수적인 기술이 되었습니다. 이 때문에 차원 축소 개념이 우리를 도와 복잡한 고차원 데이터를 손실이 적게 단순화하는 신뢰할 수 있는 접근 방식을 제공합니다. 우리의 주요 초점은 파이썬에 있으며, 간단함과 다양한 데이터 처리 라이브러리로 데이터 과학 애호가들 사이에서 인기가 있습니다.
현대 디지털 세계에서 데이터의 부피는 점점 더 커지고 이는 높은 복잡성을 동반합니다. 이러한 복잡성은 데이터의 기본 구조를 이해하는 데 도전을 제공하며, 효과적인 데이터 모델링과 시각화를 방해할 수 있습니다. 그러나 파이썬과 강력한 차원 축소 기법을 결합하여 이러한 데이터 혼돈을 의미 있는 인사이트로 변환할 수 있습니다.
파이썬 Pandas 데이터프레임으로부터 코드 없이 데이터 시각화를 빠르게 생성하고 싶나요?
PyGWalker는 시각적 탐색적 데이터 분석을 위한 파이썬 라이브러리입니다. PyGWalker (opens in a new tab)는 판다스 데이터프레임과 폴라스 데이터프레임을 Tableau 스타일의 사용자 인터페이스로 변환하여 Jupyter Notebook 데이터 분석 및 데이터 시각화 워크플로우를 간소화할 수 있습니다.
[
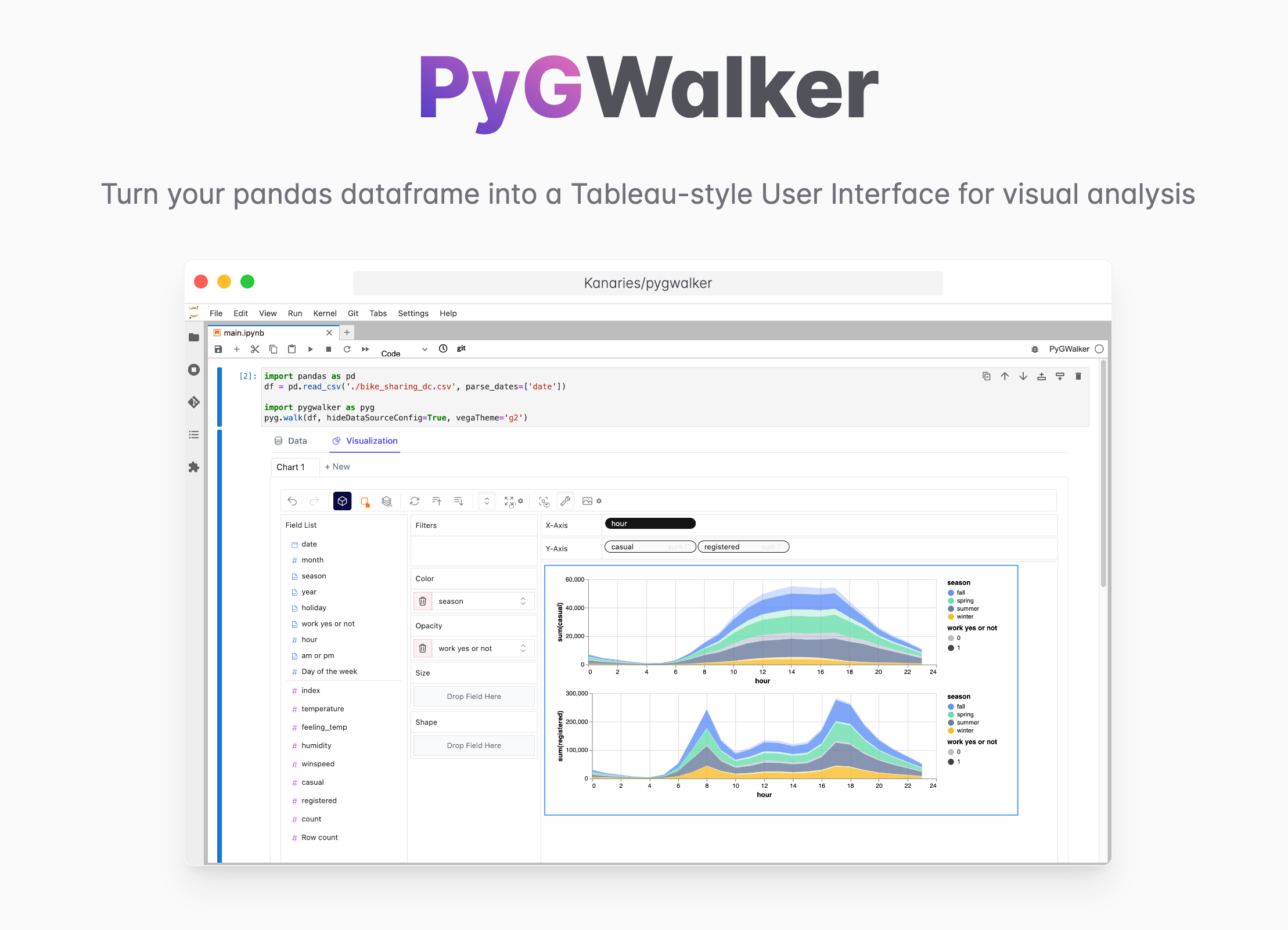](https://github.com/Kanaries/py (opens in a new tab)
gwalker)
차원 축소의 이해
기계 학습 분야에서 차원 축소는 데이터를 고차원 공간에서 저차원 공간으로 변환하는 것을 의미합니다. 목표는 중요한 정보를 최대한 보존하면서 중복성과 잡음을 제거하는 것입니다.
여러 가지 차원 축소 기법이 존재하며, 각각 고유한 강점과 적용 영역이 있습니다. 파이썬에서 가장 널리 사용되는 두 가지 기법인 주성분 분석 (PCA)와 t-분포 확률적 이웃 임베딩 (t-SNE)에 대해 자세히 살펴보겠습니다.
주성분 분석 (PCA)
PCA는 선형 차원 축소 기법입니다. 이는 데이터에서 가장 분산이 큰 방향 또는 '주성분'을 식별하여 작동합니다. 첫 번째 주성분은 최대 분산을 캡처하며, 두 번째, 세 번째 순서로 이어집니다. 파이썬에서는 sklearn 라이브러리를 활용하여 PCA를 구현할 수 있습니다.
from sklearn.decomposition import PCA
# X가 고차원 데이터셋이라고 가정합니다
pca = PCA(n_components=2) # 2차원으로 축소합니다
X_reduced = pca.fit_transform(X)이 코드 블록은 두 개의 컴포넌트를 가진 PCA 변환기를 초기화하고 데이터셋에 적용합니다. 결과는 원래 분산의 대부분을 보존한 축소된 데이터입니다.
t-분포 확률적 이웃 임베딩 (t-SNE)
PCA와 달리 t-SNE는 비선형 차원 축소 기법입니다. 이는 고차원 공간에서 저차원 공간으로의 인스턴스 근접성 유지를 기본 원칙으로 합니다. 파이썬의 sklearn 라이브러리도 t-SNE 구현을 지원합니다.
from sklearn.manifold import TSNE
# X가 고차원 데이터셋이라고 가정합니다
tsne = TSNE(n_components=2, random_state=42) # 2차원으로 축소합니다
X_reduced = tsne.fit_transform(X)여기서 TSNE 객체는 두 개의 컴포넌트로 초기화됩니다. fit_transform 함수를 사용하여 축소를 수행합니다.
PCA와 t-SNE는 강력한 도구이지만, 파이썬의 보물창고에는 이 외에도 선형 판별 분석 (L
DA), 커널 PCA, 특이값 분해 (SVD) 등을 포함하여 다른 기법들을 탐구할 것입니다.
차원 축소의 장단점
다른 기술과 마찬가지로, 차원 축소에는 장단점이 있습니다. 한편으로는 모델링의 계산 비용을 크게 줄이고, 차원의 저주를 완화하여 모델 성능을 향상시키고, 보다 간편한 데이터 시각화를 가능하게 합니다. 그러나 축소된 데이터셋은 해석 가능성을 잃을 수 있으며, 중요한 정보가 때로는 손실될 수도 있습니다. 이러한 트레이드오프에 대한 깊은 이해는 데이터 과학자가 이러한 기법을 적용할지 여부를 결정할 때 중요합니다.
실제 문제에 차원 축소 기법 적용하기
차원 축소의 실제 적용은 다양하고 넓은 범위를 가지고 있습니다. 아래에서는 파이썬의 차원 축소 기법이 중요한 역할을 하는 몇 가지 사용 사례를 살펴보겠습니다.
이미지 처리
이미지 처리에서는 각 픽셀을 특징으로 취급하는 고차원 데이터가 일반적입니다. PCA와 같은 차원 축소 기법을 적용하면 이미지 데이터의 복잡성을 크게 줄여 더 빠른 처리와 분석이 가능해집니다. 파이썬에서 이미지 압축을 위해 PCA를 사용하는 기본적인 예제를 살펴보겠습니다.
from sklearn.decomposition import PCA
from sklearn.datasets import load_sample_image
# 이미지 로드
image = load_sample_image('flower.jpg')
# 이미지 펼치기
image = image.reshape((image.shape[0], -1))
# PCA 적용
pca = PCA(n_components=100)
compressed_image = pca.fit_transform(image)위의 코드에서는 먼저 이미지 데이터를 펼칩니다. 그런 다음 PCA를 적용하여 이미지 데이터의 차원을 축소합니다.
텍스트 데이터 처리
텍스트 데이터 처리는 특히 단어 가방 (Bag of Words)이나 TF-IDF와 같은 기법을 사용할 때 고차원 데이터와 관련이 있습니다. 비선형 차원 축소 기법인 t-SNE는 자연어 처리 (NLP)에서 고차원 텍스트 데이터의 시각화에 자주 사용됩니다.
대규모 데이터셋
대규모 데이터셋의 경우, 차원 축소는 거의 필수적입니다. PCA와 같은 기법을 사용하면 중복되는 특징을 제거하여 훈련 프로세스를 가속화하고 전체적인 기계 학습 모델의 성능을 개선할 수 있습니다.
이제 파이썬에서 차원 축소에 대한 자주 묻는 질문 몇 가지에 답해보겠습니다.
자주 묻는 질문
-
Python에서 이미지 데이터에 대한 최적의 차원 축소 기법은 무엇인가요? 일반적인 답은 없지만, 계산 효율성과 데이터의 최대 분산 방향을 캡처하는 능력으로 인해 PCA가 종종 좋은 시작점입니다.
-
차원 축소를 위한 특정한 Python 라이브러리가 있나요? 예, Python에는 다양한 차원 축소 기법을 지원하는 여러 라이브러리가 있습니다. 가장 인기 있는 라이브러리는 PCA, t-SNE 등을 위한 클래스를 제공하는
sklearn입니다. -
차원 축소는 기계 학습 모델에 어떤 이점을 제공하나요? 차원 축소는 차원의 저주를 완화하여 모델 성능을 향상시키는 데 도움을 주며, 계산 요구 사항을 줄여 대규모 데이터셋 작업을 용이하게 만듭니다.
결론
이로써 파이썬에서의 차원 축소에 대한 탐색의 첫 번째 부분을 마치겠습니다. 다음 섹션에서는 더 고급 차원 축소 기법, 파이썬의 구현, 그리고 실제 사용 사례에 대해 더 깊이 알아보겠습니다.