PythonにおけるT検定とP値の探求
Published on
統計分析は、データを理解し解釈するための強力なツールです。数多く存在する統計テストの中でも、T検定とP値の概念は特に重要です。本記事では、これらの概念について深く掘り下げ、Pythonでの使用方法を探り、それらがどのように効果的なデータ分析に繋がるかを見ていきます。
T検定について理解する
T検定は、2つまたはそれ以上のグループの間の重要性を比較するための統計的な仮説検定方法です。本質的には、審査対象となるグループ間に有意な差があるかどうかを判断するのに役立ちます。これは、正規分布に従うが未確定の分散を持つデータセットで主に使用されます。
T検定における仮説の受諾
T検定には、2つのグループの平均値は等しいという帰無仮説が存在します。適用される公式に基づいて値を計算し、標準値と比較して帰無仮説を受諾または棄却します。帰無仮説が棄却される場合、データの読み取りが強固で、単なる偶然の結果ではないことを示します。
T検定を実行するための前提条件
T検定を行う前に、特定の前提条件を満たす必要があります。
- データは連続的なまたは順序尺度に従う必要があります。
- データは全ポピュレーションの一部を代表するランダムサンプルである必要があります。
- プロットされたデータは、正規または鐘型の分布になる必要があります。
- 標準偏差が近いサンプルの場合のみ分散が存在します。
使用するT検定とタイミング
データとそれに関連する問題に応じて、ペアのT検定、2つのサンプルT検定、そして1つのサンプルT検定の異なるタイプから選択できます。
P値の紹介
P値とは、観測された差が単なる偶然によって起こった可能性の確率測定値です。P値が小さい程、観測された差の統計的有意性が高いことを示します。P値は、仮説検定のための事前設定の信頼レベルに代わって提供され、異なるテストからの結果を比較する手段を提供します。
PythonによるT検定とP値の例
A/BテストのシナリオでT検定とP値を適用し、Pythonの具体的な例に飛び込んでみましょう。AとBのグループにおける顧客の注文金額を割り当てるデータを生成し、Bがわずかに高くなるようにします。
import numpy as np
from scipy import stats
A = np.random.normal(25.0, 5.0, 10000)
B = np.random.normal(26.0, 5.0, 10000)
stats.ttest_ind(A, B)出力は次のようになります:
Ttest_indResult(statistic=-14.254472262404287, pvalue=7.056165380302005e-46)ここでは、t統計量は2つの集合の差を測定する指標であり、p値は観測値が極端なt値にある確率を反映しています。同じ集合を比較する場合、t統計量は0であり、p値は1であり、帰無仮説を支持しています。
stats.ttest_ind(A, A)結果:
Ttest_indResult(statistic=0.0, pvalue=1.0)p値の有意水準は主観的であり、すべてが確率の問題であるため、実験の結果が「有意である」と断定することはできません。
T検定を使用する利点
結論として、T検定には次のような利点があります。
- 正確なテストに必要なデータが限定されている
- 形式はシンプルで理解しやすい
- 出力は簡単に解釈できる
- ストレステストや品質テストの必要性を排除し、コスト効果が高い
統計分析にPythonを活用することで、T検定とP値を効果的に活用し、データをより理解し、より正確な判断を下すことができます。
Pythonで簡単にデータ可視化を作成したいですか?
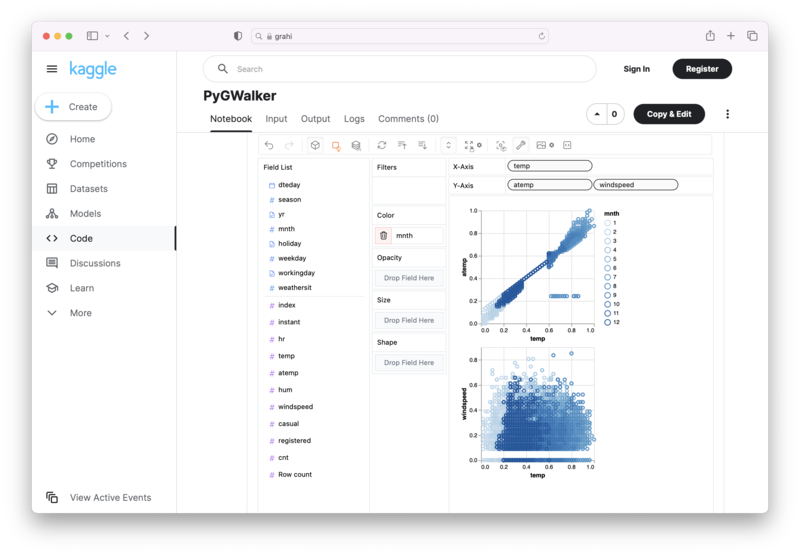
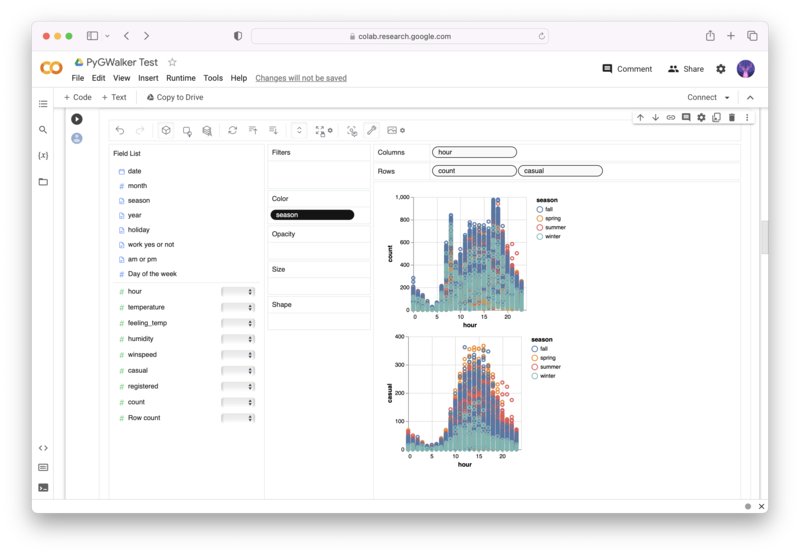
PyGWalkerは、Jupyter Notebookベースの環境内でデータ分析および可視化ワークフローをスピードアップするためのオープンソースPythonプロジェクトです。
PyGWalker (opens in a new tab)は、Pandas Dataframe(またはPolars Dataframe)をビジュアル UIに変換して、変数をドラッグアンドドロップしてグラフを簡単に作成できます。次のコードを使用して、次のようにします。
pip install pygwalker
import pygwalker as pyg
gwalker = pyg.walk(df)このオンラインノートブックでPyGWalkerをすぐに実行できます:
また、GitHubで⭐を付けてください!