Scikit-Learnとは:必須の機械学習ライブラリ
Published on
今日のデータ駆動型の世界では、機械学習がますます人気を集めています。それはデータから明示的にプログラムされずに学習することができる強力な技術です。機械学習アルゴリズムは、データ中のパターンを特定し、意思決定に役立つ予測を生成することができます。
機械学習アルゴリズムを実行するには、データモデリングや分析に使用されるツールや技術を提供するライブラリが必要です。Pythonで機械学習に使用される最も人気のあるライブラリの1つが、Scikit-LearnまたはSklearnとして知られているものです。
この記事では、Scikit-Learnとは何か、機械学習に使用する方法、およびこのライブラリを使用することの利点について探索します。
Scikit-Learnとは?
Scikit-Learnは、Pythonでの機械学習のためのオープンソースライブラリです。Pythonの数値計算や科学計算の人気ツールであるNumPy、SciPy、Matplotlibライブラリの上に構築されています。
Scikit-Learnは、分類、回帰、クラスタリング、次元削減のアルゴリズムなど、機械学習の幅広いツールを提供しています。また、データの正規化、スケーリング、エンコーディングなどの前処理ツールの範囲も含まれています。
Scikit-Learnは、機械学習モデルの構築においてシンプルかつ効率的に設計されています。使いやすく一貫性のあるAPIを備えており、初心者から経験豊富な機械学習実践者まで人気があります。
Scikit learnとsklearn
Scikit-learnとSklearnは、データサイエンティストや機械学習実践者によく使用されている2つの人気のある機械学習フレームワークです。両者の主な違いは、Scikit-Learnがパッケージの元の名前であるのに対し、Sklearnがユーザーの間で一般的に使用されている略称であるということです。
Scikit-Learnは、回帰、分類、クラスタリング、次元削減などの様々なタスクを実行できるオープンソースの機械学習ライブラリです。 NumPy、SciPy、Matplotlibなどの他の一般的に使用されるPythonライブラリの上に構築されており、データ分析や可視化に必要な重要なライブラリです。Scikit-Learnは、パフォーマンスとスケーラビリティに最適化された最適化されたコードで使用しやすいように設計されています。
一方、Sklearnは、データサイエンティストがよく使用する一般的な略称です。パッケージはScikit-Learnと同じで、より簡単に打ち込めるようにSklearnと言及されています。2つのパッケージは、同じ機能、ドキュメント、およびサポートを持ち、同一です。
Python Pandasデータフレームからコードなしでデータ可視化を迅速に作成するには?
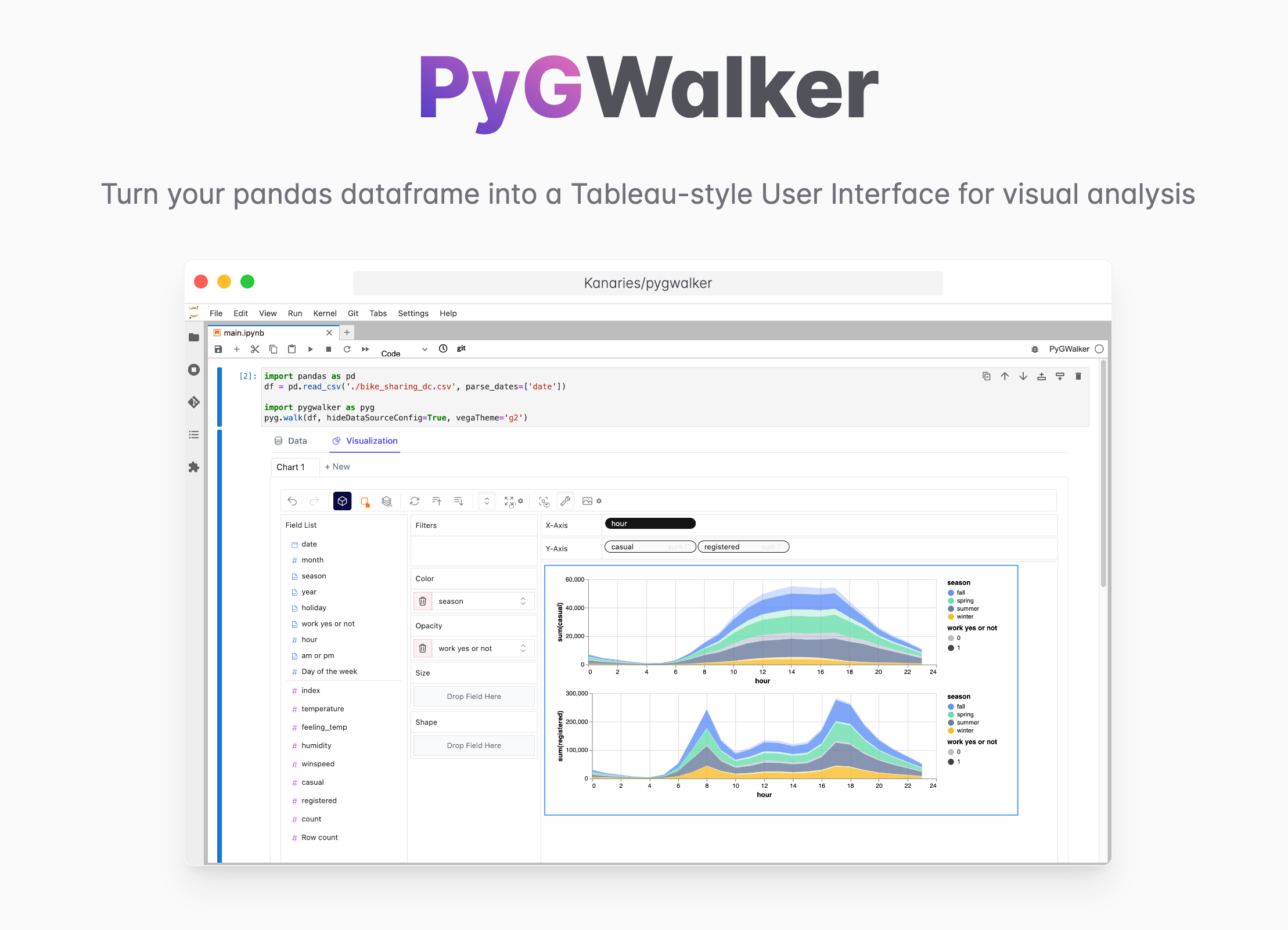
PyGWalkerは、可視化を伴った探索的データ分析のためのPythonライブラリです。 PyGWalker (opens in a new tab)は、pandasデータフレーム(および極座標データフレーム)をTableauスタイルのユーザーインターフェースに変換し、視覚的な探索のために簡素化できます。
Scikit-Learnをどのように機械学習に使用できるか?
Scikit-Learnは、分類、回帰、クラスタリング、次元削減などの幅広い機械学習タスクに使用できます。
- 分類:Scikit-Learnは、ロジスティック回帰、決定木、サポートベクターマシンなどの人気のある分類アルゴリズムを提供しています。
- 回帰:Scikit-Learnは、線形回帰やリッジ回帰などのさまざまな回帰アルゴリズムも提供しています。
- クラスタリング:Scikit-Learnは、データポイントをグループ化するためのk-meansクラスタリングや階層クラスタリングなどの異なるクラスタリングアルゴリズムを提供しています。
- 次元削減:Scikit-Learnは、主成分分析(PCA)やt-distributed Stochastic Neighbor Embedding(t-SNE)などの高次元データの次元削減に使用されるさまざまな技術を提供しています。
- 前処理:Scikit-Learnは、データの正規化、スケーリング、エンコーディングなどの前処理に使用できるさまざまなツールを提供しています。
Scikit-Learnを機械学習に使用するには、まずライブラリから関連モジュールをインポートする必要があります。以下は、Scikit-LearnをインポートしてIrisデータセットをロードする基本的な例です。
import sklearn
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
```上記の例は、分類タスクに使用される人気のあるデータセットであるアヤメデータセットの読み込みを示しています。 次に、入力属性を `X` に割り当て、出力クラスラベルを `y` に割り当てます。
## Scikit-Learnが提供するアルゴリズムの種類は何ですか?
Scikit-Learnは、機械学習のための幅広いアルゴリズムを提供しています。 以下は、最も人気のあるアルゴリズムの一部です。
### ロジスティック回帰
ロジスティック回帰は、分類タスクに使用される人気のあるアルゴリズムです。 1つ以上の予測変数に基づいてバイナリまたはマルチクラスの応答変数の確率を推定します。
以下は、Scikit-Learnでロジスティック回帰モデルを適合させる方法の例です。
```python
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=0).fit(X, y)サポートベクターマシン(SVM)
サポートベクターマシンは、分類、回帰、外れ値検出に使用される一連の教師あり学習手法です。 SVMは高次元空間でも効果的で、メモリ効率に優れています。
以下は、Scikit-LearnでSVMモデルを適合させる方法の例です。
from sklearn.svm import SVC
clf = SVC(kernel='linear', C=1, random_state=0)
clf.fit(X, y)決定木
決定木は、分類と回帰の両方のタスクで使用される人気のあるアルゴリズムです。 決定とその可能な結果のツリー状のモデルを作成します。
以下は、Scikit-Learnで決定木モデルを適合させる方法の例です。
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier().fit(X, y)機械学習にScikit-Learnを使用する利点
Scikit-Learnには、機械学習モデルを構築するための人気のある選択肢である多くの利点があります。
- オープンソース:Scikit-Learnは無料で使用できるオープンソースのソフトウェアです。
- 簡単さ:Scikit-Learnはシンプルで使いやすいように設計されています。 異なるアルゴリズム間で簡単に切り替えることができる一貫したAPIを持っています。
- 効率:Scikit-Learnはパフォーマンスと効率のために構築されています。 大規模なデータセットに最適化されており、マルチコアCPUとGPUを利用できます。
- 人気:Scikit-Learnは、学術界や産業界の両方で広く使用されているため、活発なコミュニティと多数のリソースが利用可能です。
結論
この記事では、Scikit-Learnとは何か、機械学習にどのように使用できるか、このライブラリを使用する利点について説明しました。 Scikit-Learnは、分類、回帰、クラスタリング、次元削減アルゴリズムを含む、機械学習のための多くのツールと技術を提供しています。 シンプルで効率的に設計されており、機械学習モデルを構築する人気の選択肢です。
Scikit-Learnについてさらに学びたい場合は、チュートリアル、ドキュメント、サンプルコードなど、オンラインで多数のリソースが利用可能です。 Scikit-Learnを使用すると、機械学習の力を活用して、予測モデルを構築し、データから洞察を見つけることができます。
さらに読む:> - Catboost:Pythonにおける革新的なデータ分析ツール
- Pythonにおける次元削減技術:簡単な紹介
- 物体検出のためのFastおよびFaster R-CNNのアーキテクチャと効率の解説
- PythonでのNLTKトークナイズの理解:包括的ガイド
- Python KNN:sklearnでK最近傍回帰のマスタリング
- Python SVM、その使い方とは
- Scikit-Learnとは何か:必須の機械学習ライブラリの紹介
- XGBoostとは何か:機械学習アルゴリズムのパワーハウス
- RおよびPythonにおける自動ARIMA:時系列予測への効率的なアプローチ
- Rにおける交差検証:包括的ガイド
- Lasso回帰対Ridge回帰:解説!
- Rにおける最尤推定:正規分布および指数分布による理解
- Rにおけるロジスティック回帰方程式:例を交えた理解
- RプログラミングにおけるKNN関数:初心者向けガイド
- Rでデータを要約する:テクニックとベストプラクティス